Dazu Zahlensalat. Oder: Wie viele Fleischklöße passen in den Topf? – Etwas Hobbymathematik für Hobbyköche

Als ich neulich den Artikel zu Königsberger Klopse geschrieben habe, fiel mir auf, dass ich einige Wissenslücken hatte, wenn es um den Durchmesser der Klöße und deren Anzahl in Bezug zum Topfdurchmesser u.s.w. geht. Das sind doch alles nur Zahlen und da muss es doch Formeln geben. Konkret stellte ich mir folgende Frage. Ich habe einen Topf mit einem bestimmten Durchmesser und eine Menge Fleischteig. Dann kann ich aus dem Teig wenige große Bällchen formen, oder viele keine Bällchen. Ich stelle folgende Rahmenbedingung: Die Klöße sollen alle die gleiche Größe haben und müssen nebeneinander im Topf Platz finden und dürfen nicht über einander liegen. Die Klöße sollen in einer Brühe garziehen, die die Bällchen gerade umschließt. Wieviel Brühe brauche ich, sodass nach dem Einlegen der Klöße der Pegel genau die Kloßdicke ist? Ziel ist es, mit möglichst wenig Brühe auszukommen. Konzentrieren wir uns auf die Anzahl der Klöße. Für einen gegebenen Topfdurchmesser und einer gegebenen Menge Fleischteig gibt es eine mathematisch definierte Anzahl, in die man den Teig teilen muss, um die Klöße zu formen, sodass die Klöße nebeneinander in den Topf passen, und die Flüssigkeitsmenge, mit der man die Zwischenräume füllen kann, minimal ist. Es kommt heraus, dass manche Kloßanzahlen dabei tabu sind und grundsätzlich nicht zu einem optimalen Verhältnis zwischen Fleisch und Brühe führen. Die Reihe dieser „schlechten Zahlen“ beginnt mit 2, 5, 6, 10, 11, 13, 15, 16, 17, 18, 25, 29, 32, 34, 35, 36 … Die anderen „guten Zahlen“ sind 1, 3, 4, 7, 8, 9, 12, 14, 19, 20, 21, 22, 23, 24, 26, 27, 28, 30, 31, 33, 37 … Also z.B. sollte man niemals 10 Klöße formen. Aus der gleichen Menge Teig kann man besser 12 Klöße machen. Habt Ihr das gewusst?

Mathematisch geht es zunächst um Kreise und nicht um Kugeln. Man versucht eine gegebene Anzahl von gleichgroßen Kreisen so nebeneinander anzuordnen, dass sie von einem möglichst kleinen größeren Kreis umschlossen werden können. Solche optimalen Anordnungen spielen eine Rolle, wenn man mehradrige Kabel konzipieren will oder Drahtseile. Am besten googled man nach „Circles in a Circle“ wenn man nach Informationen dazu sucht. Man findet dann Angaben zu den Durchmessern der inneren und äußeren Kreise, und Zeichnungen, wie die inneren Kreise anzuordnen sind. Dabei geht man entweder davon aus, dass die inneren Kreise den Durchmesser 1 haben, und macht Angaben zum Durchmesser des umschließenden Kreises, oder man geht von einem fixen Außenkreis mit Durchmesser 1 aus und redet über die maximal möglichen Durchmesser der inneren Kreise. Eigentlich ist das egal, man muss dann nur den Kehrwert bilden. Zwei Kreise mit Durchmesser 1 kann man mit einem Kreis von Durchmesser 2 umschließen. Der Kehrwert wäre 1/2. Zwei Kreise mit Durchmesser 1/2 passen optimal in einen Umkreis mit Durchmesser 1. In dieser Diskussion ist es auch egal ob wir grundsätzlich über den Durchmesser sprechen oder grundsätzlich über den Radius. Die Verhältnisse zwischen Außenkreis und Innenkreise bleiben die gleichen. Die Mathematik neigt dazu den Radius zu bevorzugen. Wir Köche messen aber lieber den Durchmesser; bei einem Topf, bei einem Fleischbällchen.

Eine umfangreiche Zusammenstellung über die Möglichkeiten, Kreise in unserem Sinne optimal anzuordnen, hat Eckard Specht von der Universität Magdeburg zusammengestellt. Man schaue sich mal die Anordnungen für 1 bis 12 Kreise und für 13-24 Kreise an. Man sieht, dass es für größere Zahlen immer unsystematischer wird. Nur ab und zu trifft man auf Konstellationen die man als homogen und ordentlich bezeichnen kann. Z.B. bei der Zahl 61. Doch will man nur einen einzigen weiteren Kreis unterbringen, fängt wieder das Geschiebe und Getrickse an. Uns interessiert für jede Kreisanzahl die bei Specht angegebene Zahl „Radius“, die für uns aber der Durchmesser der Kreise ist, weil wir von einem umschließenden Kreis mit Durchmesser 1 ausgehen. Für die Anzahl n=12 haben wir z.B. die Größe 0.248163. Was können wir damit anfangen. Beziehen wir das auf einen Topf von 25 cm Durchmesser, rechnen wir 0,248163 x 25cm und erhalten ungefähr 6,204cm . Das ist der Durchmesser eines Fleischbällchens um 12 Stück davon gerade noch in den Topf hineinzubekommen.

Für die Anzahlen 1 bis 40 haben wird folgende Tabelle:

n	d	v = 2/3 * n * d^3	w = d – v
1	1.000000	0.666667	0.333333
2	0.500000	0.166667	0.333333
3	0.464102	0.199926	0.264176
4	0.414214	0.189514	0.224699
5	0.370192	0.169106	0.201086
6	0.333333	0.148148	0.185185
7	0.333333	0.172840	0.160494
8	0.302593	0.147767	0.154827
9	0.276769	0.127204	0.149564
10	0.262259	0.120254	0.142005
11	0.254855	0.121389	0.133466
12	0.248163	0.122265	0.125898
13	0.236068	0.114015	0.122053
14	0.231031	0.115092	0.115938
15	0.221173	0.108192	0.112981
16	0.216665	0.108491	0.108174
17	0.208680	0.102991	0.105689
18	0.205605	0.104299	0.101306
19	0.205605	0.110093	0.095511
20	0.195224	0.099206	0.096018
21	0.190392	0.096622	0.093770
22	0.183833	0.091118	0.092715
23	0.180336	0.089926	0.090410
24	0.176939	0.088632	0.088307
25	0.173828	0.087540	0.086288
26	0.171580	0.087556	0.084025
27	0.169308	0.087358	0.081950
28	0.166253	0.085777	0.080475
29	0.162904	0.083579	0.079324
30	0.161349	0.084010	0.077339
31	0.158945	0.082986	0.075958
32	0.155534	0.080267	0.075267
33	0.154162	0.080603	0.073559
34	0.151264	0.078450	0.072814
35	0.149317	0.077679	0.071638
36	0.148219	0.078150	0.070070
37	0.147956	0.079893	0.068063
38	0.143639	0.075078	0.068561
39	0.141686	0.073952	0.067734
40	0.140374	0.073761	0.066613

„d“ ist der Durchmesser eines Kloßes auf Grund der Angaben, die wir bei Specht finden. Die Spalte „v“ ist eine relative Angaben für das Volumen der Klöße (aller n vielen Klöße zusammen) und „w“ eine entprechende Zahl für die benötigte Menge Brühe um die Klöße zu umschließen. Insgesamt ist der Topf ja bis zu Höhe d gefüllt (mit Brühe und Klöße). v und w sind letztlich auch Höhenangaben. Nehme ich die Klöße aus der Brühe heraus sinkt der Flüssigkeitspegel um den Wert v auf den Wert w. Es gilt also d=v+w. Auf unsere 12 Klöße im Topf mit 25cm Durchmesser hochgerechnet ergibt das, dass wir zunächst Brühe bis zu Höhe 0.125898 x 25cm, also etwa 3,147cm in den Topf geben müssen. Dann geben wir die Klöße hinein und der Pegel steigt um 0.122265 x 25cm = 3,056cm auf die Kloßdicke von 6,204cm.

Aber wie viel Kloßteig und wie viel Brühe ist denn das in Kubikzentimetern (ccm = Milliliter). Dazu rechnen wir den Inhalt unseres 25cm Topfes bis zur Höhe 25cm aus. Wir rechnen Kreisfläche mal Höhe also Pi/4 mal 25cm hoch 3. Das sind 12271,846 ccm, also etwa 12 Liter. Jetzt müssen wir nur noch unsere relativen Volumina v und w mit diesem Referenzvolumen multiplizieren. 12271,846ccm * 0,122265 = 1500,417ccm (das ist der Kloßteig) und 12271,846 ccm * 0,125898 = 1545,001ccm (das ist die benötigte Brühe).

Das wäre also eine optimale Lösung, wenn man etwa 1,5 Liter Fleischteig hat. Dann mache ich 12 Klöße von gut 6cm Durchmessern und ich brauche 1,5 Liter Brühe mit einem kleinen Nachschlag, um die Klöße garen zu können. Der Ausgangspunkt dieses Beispiel war die Zahl 12. Jetzt gehen wir mal von einen gegebenen Fleischteigmenge aus. Sagen wir 1 Liter also 1000ccm. Wir bleiben bei dem Topf mit 25cm Durchmesser. Wir rechnen erstmal das relative Volumen des Fleischteiges aus: 1000ccm geteilt durch 12271,846ccm. Das sind etwa 0,081487. In unserer Tabelle suchen wir die größte Zahl n, bei der Wert v größer oder gleich 0,081487 ist. Das ist die Zahl n=31. Wir müssen also den Fleischteig in 31 gleich große Teile teilen und daraus die Klöße rollen.

Wir sehen, dass die Werte „v“ in der Tabelle in der groben Tendenz fallend sind. Trotzdem pendelt der Wert etwas hin und her. Immer wieder gibt es Werte, die von einem späterem Wert nochmal übertroffen werden. Diese scheiden für unsere Betrachtung aus. Wir haben die brauchbaren Kloßanzahlen in der Tabelle hervorgehoben. Es sind 1, 3, 4, 7, 8, 9, 12, 14, 19, 20, 21, 22, 23, 24, 26, 27, 28, 30, 31, 33, 37, …

Die Anzahl 31 aus dem letzten Beispiel ist immer die Zahl der Wahl, wenn das errechnete relative Volumen des Fleischteiges größer als 0,080603 und kleiner gleich 0,082986 ist. Für Kleinere Mengen sind 33 Klöße besser. Und unter 0,079893 sogar 37 Klöße. Aber bitte niemals 32, 34, 35 oder 36 Klöße. Bei einer größeren Mengen als 0,082986 werden die Klöße zu dick, sodass 31 Stück davon nicht mehr in den Topf passen. Dann forme ich 30 oder 28 Klöße. Die werden zwar noch etwas dicker, aber es sind ja weniger Klöße. Und dann passen sein.

Die obere Grenze an Fleischteig in ccm gemessen, damit 31 Klöße im 25cm-Topf geeignet ist, berechnet sich in ccm durch 0,082986 * 12271,846ccm = 1018,391ccm. Für diese Teigmenge würden wir eine Flüssigkeitsmenge von 0,075958 * 12271,846ccm = 932.145ccm benötigen. Wir sind aber weniger Teig ausgegangen (1000ccm) und somit werden die 31 Klöße etwas kleiner. Sie liegen also etwas lockerer im Topf, wodurch wir mehr Flüssigkeit als Füllmenge brauchen. Der Mehrverbrauch reduziert sich aber, weil der Topf ja nicht ganz so hoch gefüllt werden muss. Es sind ja kleinere Klöße.

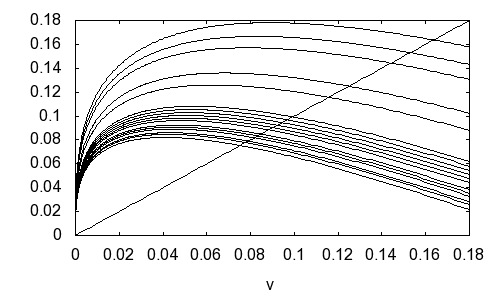
Das müssen wir nochmal genauer betrachten. Wie nämlich variiert die benötigte Flüssigkeit, wenn wir die Kloßteigmenge variieren und von einer festen Anzahl Klöße ausgehen. Die Formel für den relativen Durchmesser eines Kloßes ist die dritte Wurzel aus 3/2 mal v/n, wenn v ein gegebenes relatives Volumen ist und n die Anzahl der Bällchen, in die wir diesen Volumen teilen. Ich erinnere an d=v+w. Also ziehen wir von dieser Wurzel nochmal den Wert v ab und erhalten die Wassermenge w. Für die Beispiele n=7, 8, 9, 12, 14, 19, 20, 21, 22, 23, 24, 26, 27, 28, 30, 31, 33 ergeben sich folgende Kurven:

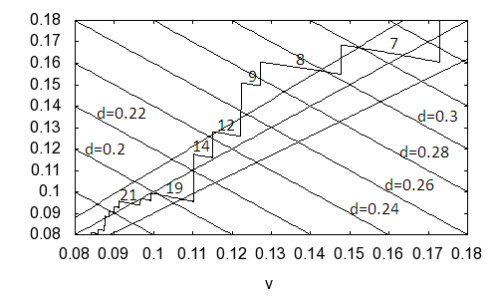
Die Kurvenschar stellt den Flüssigkeitsbedarf in Abhängigkeit zur Fleischteigmenge dar. Jede einzelne Kurve fixiert ein Kloßanzahl. Die Kurve für n=7 ist ganz oben im Bild. Mit größerem n liegen die Kurven immer tiefer, und zunehmend dichter beieinander. Die Kurven berücksichtigen nicht, dass mit steigender Kloßteigmenge und damit steigender Kloßdicke, die Klöße ab einer Stelle eigentlich den Topfrand durchbrechen. Für unsere Betrachtung ist die Kurve dann nicht mehr relevant. Eine ideale Kurve für die jeweils minimal benötigte Menge von Brühe muss also immer wieder einen Sprung zur nächst kleineren „guten“ Kloßanzahl machen. So erhalten wir eine Treppenfunktion, die im folgenden Bild dargestellt wird.

Waagerecht ist die Kloßteigmenge aufgetragen und senkrecht die benötigte Menge Brühe. Die eingezeichnete Diagonale von links unten nach rechts oben stellt den Gleichstand dar: also genauso viel Brühe, wie Fleischteig. Die beiden Geraden daneben stehen für 10% mehr Brühe und 10% weniger Brühe. Dadurch kann man die Pendelbewegung der Treppenkurve besser einschätzen. Die Zahlen auf den Stufen sind die Kloßanzahlen. Die schrägen Linien von links oben nach rechts unten kennzeichnen den Kloßdurchmesser.

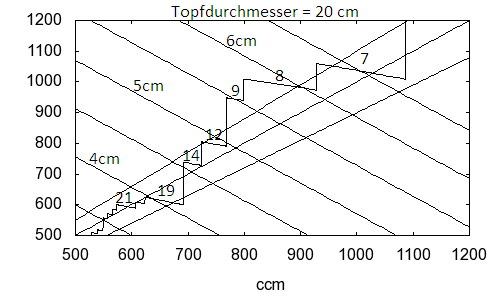
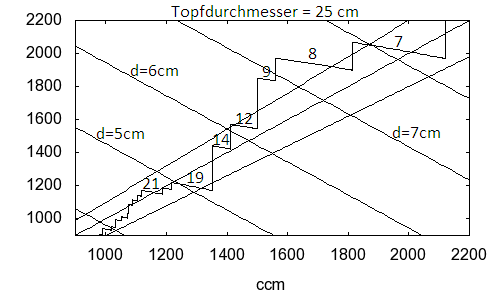
Zum Schluss wollen wir die letzte Graphik mit den relativen Werten noch auf Zentimeter und Kubikzentimeter zweier realer Töpfe skalieren: nämlich Töpfe mit 20 cm und 25 cm Durchmesser. Alle relativen Längenangaben müssen wir dann mit dem Topfdurchmesser multiplizieren. Und alle relativen Volumenangaben multiplizieren wir mit dem Rauminhalt des Topfes, den wir uns so hoch denken, wie der dick ist. Das sind dann 6283 ccm bei dem 20 cm Topf und 12272 ccm bei dem 25 cm Topf. So erhalten wir folgende beiden Bilder: